F Times G Of X
zacarellano
Sep 14, 2025 · 7 min read
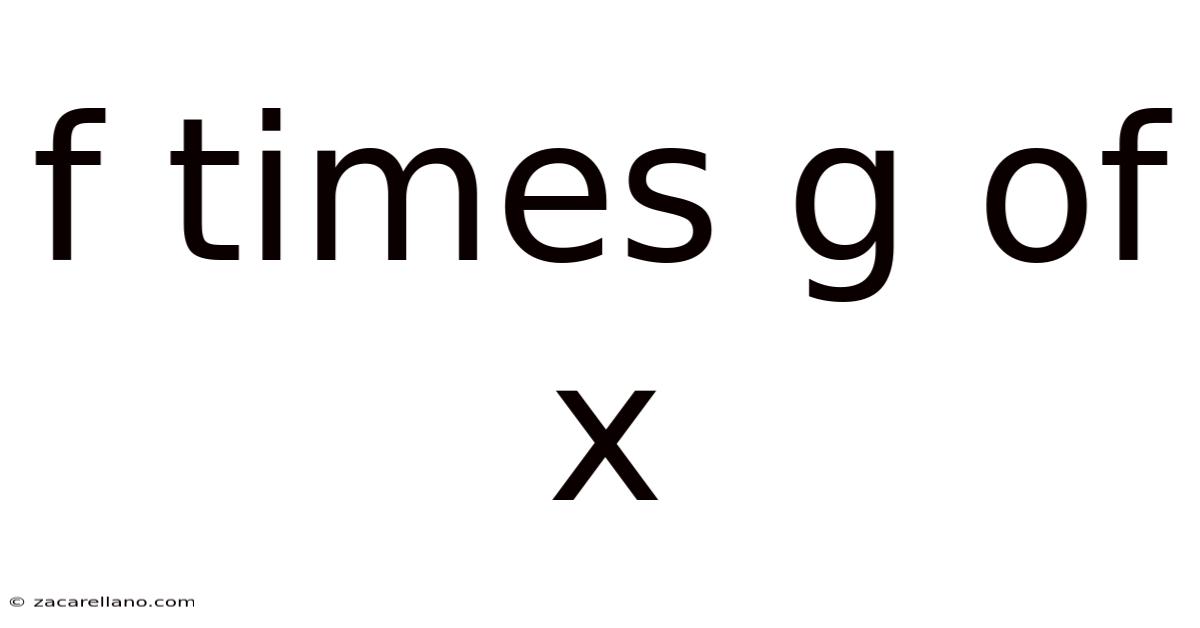
Table of Contents
Decoding the Mystery of f(x) * g(x): A Deep Dive into Function Multiplication
Understanding how to multiply functions, often represented as f(x) * g(x), is a fundamental concept in mathematics, particularly in calculus and higher-level math courses. While the notation might seem intimidating at first, the underlying principle is surprisingly straightforward. This article will guide you through a comprehensive exploration of function multiplication, covering its definition, practical applications, examples, and frequently asked questions. We'll demystify this important concept, equipping you with the knowledge and confidence to tackle related problems.
Introduction: What Does f(x) * g(x) Mean?
In essence, f(x) * g(x) represents the pointwise multiplication of two functions, f(x) and g(x). This means that for every value of x within the domain of both functions, you multiply the corresponding output values of f(x) and g(x) to obtain the output of the new function, often denoted as (f*g)(x) or simply f(x)g(x). It's crucial to remember that this operation is defined only for the values of x where both f(x) and g(x) are defined. The resulting function inherits the domain that is the intersection of the domains of f(x) and g(x).
Let's break this down further. Imagine f(x) as a machine that takes an input (x) and produces an output (f(x)). Similarly, g(x) is another machine with its own input (x) and output (g(x)). f(x) * g(x) is like connecting these two machines: the input (x) goes into both machines simultaneously, producing outputs f(x) and g(x). These outputs are then multiplied together to generate the final output of the combined machine (f*g)(x).
Understanding the Domain and Range
The domain of the resulting function (fg)(x) is critically important. It’s simply the set of all x-values for which both f(x) and g(x) are defined. If f(x) is undefined for a certain x-value, or if g(x) is undefined, then (fg)(x) is also undefined at that point. The range, however, is less straightforward to determine and often requires careful analysis of the individual functions and their behaviors.
Example:
Let's consider f(x) = x² and g(x) = x + 1.
- Domain of f(x): All real numbers (-∞, ∞).
- Domain of g(x): All real numbers (-∞, ∞).
- Domain of (f*g)(x): Since both functions are defined for all real numbers, the domain of (f*g)(x) is also all real numbers (-∞, ∞).
- (f*g)(x) = f(x) * g(x) = x²(x + 1) = x³ + x²
In this case, (f*g)(x) is a simple polynomial function. However, other combinations can lead to more complex results, including piecewise functions or functions with restricted domains.
Step-by-Step Guide to Multiplying Functions
The process of multiplying functions is generally straightforward:
- Identify the functions: Clearly define the functions f(x) and g(x).
- Determine the domain: Find the domain of each individual function. The domain of (f*g)(x) will be the intersection of these domains.
- Multiply the expressions: Substitute the expressions for f(x) and g(x) into the expression f(x) * g(x).
- Simplify (if possible): Simplify the resulting expression by combining like terms, expanding brackets, or factoring.
- State the resulting function: Write down the simplified expression for (f*g)(x), including its domain.
Illustrative Examples
Let's delve into a few more examples to solidify our understanding:
Example 1: Polynomial Functions
f(x) = 2x + 3 and g(x) = x² - 1.
(f*g)(x) = (2x + 3)(x² - 1) = 2x³ - 2x + 3x² - 3 = 2x³ + 3x² - 2x - 3
The domain of both f(x) and g(x) is all real numbers, so the domain of (f*g)(x) is also all real numbers.
Example 2: Rational Functions
f(x) = 1/x and g(x) = x + 2.
(f*g)(x) = (1/x)(x + 2) = (x + 2)/x
The domain of f(x) is all real numbers except x = 0. The domain of g(x) is all real numbers. Therefore, the domain of (f*g)(x) is all real numbers except x = 0.
Example 3: Functions with Restricted Domains
f(x) = √x and g(x) = x - 4.
(f*g)(x) = √x(x - 4) = x√x - 4√x
The domain of f(x) is x ≥ 0. The domain of g(x) is all real numbers. The intersection of these domains is x ≥ 0. Therefore, the domain of (f*g)(x) is x ≥ 0.
Applications of Function Multiplication
Function multiplication isn't just a theoretical exercise; it has numerous applications in various fields:
- Calculus: Finding derivatives and integrals often involves multiplying functions. The product rule for differentiation is a prime example.
- Physics and Engineering: Many physical phenomena are modeled using functions, and multiplying functions can represent the combined effects of multiple factors. For example, in electrical circuits, the voltage across a resistor can be a function of current, and the power dissipated can be found by multiplying the voltage and current functions.
- Economics and Finance: Models in economics frequently employ functions to represent relationships between variables. Multiplying functions might represent interactions between market forces or the combined effect of multiple economic factors.
- Computer Science: Function multiplication is used extensively in algorithms and programming, particularly when dealing with data processing and transformations.
The Scientific Explanation: Why Does Pointwise Multiplication Work?
The validity of pointwise multiplication stems from the fundamental properties of real numbers. Multiplication is a binary operation defined on real numbers, meaning it takes two real numbers as inputs and produces a single real number as an output. Since f(x) and g(x) produce real number outputs for any x in their common domain, we can apply the multiplication operation to their outputs. This pointwise approach ensures that the resulting function (f*g)(x) is also well-defined for each x in the common domain. This aligns with the basic principles of function composition and operation, providing a solid mathematical foundation for this process.
Frequently Asked Questions (FAQ)
Q1: Can I multiply functions with different domains?
A1: You can perform the multiplication, but the domain of the resulting function (fg)(x) will be the intersection of the domains of f(x) and g(x). Any x-values where either f(x) or g(x) is undefined will be excluded from the domain of (fg)(x).
Q2: What if one of the functions is a constant?
A2: If one of the functions, say g(x), is a constant function (e.g., g(x) = c, where c is a constant), then (f*g)(x) = cf(x). This simply scales the output of f(x) by the constant factor c.
Q3: Is function multiplication commutative and associative?
A3: Yes, function multiplication is both commutative and associative. This means that f(x) * g(x) = g(x) * f(x) (commutative property) and (f(x) * g(x)) * h(x) = f(x) * (g(x) * h(x)) (associative property), provided that the domains are appropriately considered.
Q4: How does function multiplication relate to other function operations?
A4: Function multiplication is one of several ways to combine functions. Others include function addition (f(x) + g(x)), function subtraction (f(x) - g(x)), function division (f(x) / g(x)), and function composition (f(g(x))). Each operation has its own rules and interpretations.
Q5: Can I multiply functions graphically?
A5: While not a direct graphical multiplication, you can visualize the result by considering the y-values (outputs) of f(x) and g(x) at each x-value. You can then plot the product of these y-values to obtain a visual representation of (f*g)(x). However, this approach is generally less efficient than algebraic manipulation.
Conclusion: Mastering Function Multiplication
Understanding function multiplication is a crucial stepping stone in your mathematical journey. It's a fundamental concept that underpins more advanced topics in calculus and related fields. By understanding the process, the domain considerations, and the practical applications, you can confidently approach problems involving the multiplication of functions. Remember the key takeaway: it's a pointwise operation, meaning you multiply the outputs of the individual functions for each value of x in their common domain. This seemingly simple concept unlocks a world of possibilities in mathematical modeling and problem-solving. Through practice and a solid grasp of the underlying principles, you'll find that function multiplication becomes an intuitive and powerful tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
Graph Of Cosecant And Secant
Sep 14, 2025
-
What Is A Proton Acceptor
Sep 14, 2025
-
Is 1 2 Greater Than
Sep 14, 2025
-
Monomers Of Nucleic Acids Are
Sep 14, 2025
-
Lcm Of 12 And 7
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about F Times G Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.