Gcf For 14 And 28
zacarellano
Sep 23, 2025 · 6 min read
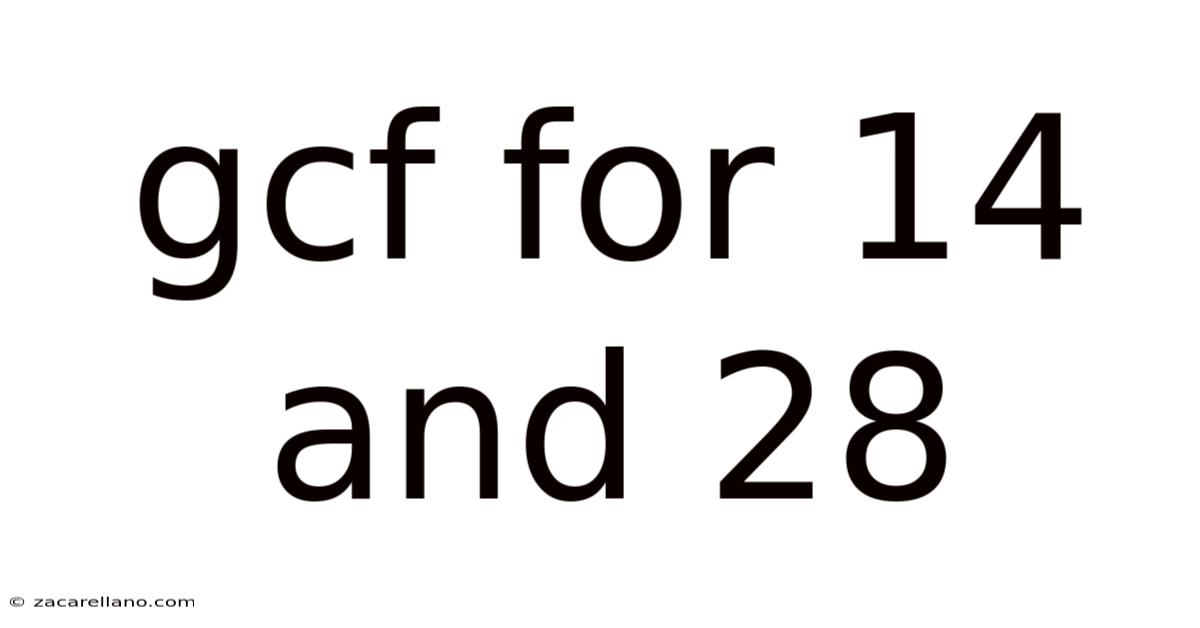
Table of Contents
Finding the Greatest Common Factor (GCF) of 14 and 28: A Comprehensive Guide
Understanding the greatest common factor (GCF), also known as the greatest common divisor (GCD), is a fundamental concept in mathematics with applications extending far beyond simple arithmetic. This article will explore the GCF of 14 and 28 in detail, explaining various methods to calculate it and providing a deeper understanding of its significance in different mathematical contexts. We'll cover different approaches, from simple listing to prime factorization, making this a complete guide for students and anyone looking to refresh their understanding of this crucial concept.
Introduction to Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It's the highest number that is a factor of all the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, so the GCF of 12 and 18 is 6.
This concept is vital in various mathematical operations, including simplifying fractions, solving algebraic equations, and understanding number theory principles. Understanding how to find the GCF is essential for building a solid foundation in mathematics.
Method 1: Listing Factors
The most straightforward method to find the GCF of 14 and 28 is by listing all the factors of each number and then identifying the largest common factor.
Factors of 14: 1, 2, 7, 14
Factors of 28: 1, 2, 4, 7, 14, 28
By comparing the two lists, we can see that the common factors are 1, 2, 7, and 14. The greatest of these common factors is 14. Therefore, the GCF of 14 and 28 is 14.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger and have more factors.
Method 2: Prime Factorization
Prime factorization is a more systematic and efficient method, especially when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 14: 2 x 7 (2 and 7 are prime numbers)
-
Prime Factorization of 28: 2 x 2 x 7 (or 2² x 7)
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. Both 14 and 28 share a prime factor of 2 (to the power of 1) and a prime factor of 7 (to the power of 1).
To find the GCF, we multiply these common prime factors together: 2 x 7 = 14. Therefore, the GCF of 14 and 28 is 14.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 14 and 28:
-
Start with the larger number (28) and the smaller number (14).
-
Subtract the smaller number from the larger number: 28 - 14 = 14
-
Replace the larger number with the result (14) and keep the smaller number (14). Now we have the numbers 14 and 14.
-
Since both numbers are equal, the GCF is 14.
The Euclidean algorithm provides a concise and efficient way to find the GCF, especially when dealing with larger numbers where other methods become less practical.
Understanding the Significance of GCF
The GCF has many important applications in mathematics and beyond:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 28/14 can be simplified by dividing both the numerator and denominator by their GCF (14), resulting in the simplified fraction 2/1 or simply 2.
-
Algebraic Expressions: GCF is used to factor algebraic expressions. For instance, the expression 14x + 28 can be factored as 14(x + 2), where 14 is the GCF of 14 and 28.
-
Number Theory: GCF plays a significant role in number theory, particularly in concepts like modular arithmetic and the study of prime numbers.
-
Real-World Applications: GCF has practical applications in various fields, such as dividing items into equal groups, determining the size of the largest square tile that can perfectly cover a rectangular area, and solving problems related to measurement and proportions.
GCF in Different Contexts
Let's explore a few examples demonstrating the application of GCF:
Example 1: Simplifying Fractions
To simplify the fraction 28/14, we find the GCF of 28 and 14, which is 14. Dividing both the numerator and denominator by 14 gives us the simplified fraction 2/1, or 2.
Example 2: Factoring Algebraic Expressions
Consider the algebraic expression 14x + 28y. The GCF of 14 and 28 is 14. We can factor out the GCF to get 14(x + 2y).
Example 3: Real-World Problem
Imagine you have 28 red marbles and 14 blue marbles. You want to divide them into identical bags, each with the same number of red and blue marbles. The GCF (14) determines the maximum number of bags you can create while ensuring each bag has an equal number of both colors. Each bag will contain 2 red marbles and 1 blue marble (28/14 = 2 and 14/14 = 1).
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. This indicates that they don't share any common factors other than 1.
Q: Can the GCF of two numbers be larger than either of the numbers?
A: No, the GCF can never be larger than the smaller of the two numbers. It's always a factor of both numbers.
Q: Is there a limit to how many methods can be used to find the GCF?
A: While the methods presented here are the most common, there are other algorithms and techniques for finding the GCF, some more suitable for computer applications and dealing with extremely large numbers.
Q: How do I find the GCF of more than two numbers?
A: To find the GCF of more than two numbers, you can extend any of the methods discussed. For example, using prime factorization, find the prime factorization of each number and then identify the common prime factors with the lowest powers. The Euclidean algorithm can also be adapted for more than two numbers.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with wide-ranging applications. Whether you use the listing method, prime factorization, or the Euclidean algorithm, understanding the concept of GCF is vital for simplifying fractions, factoring algebraic expressions, and solving various mathematical problems. This article has provided a thorough exploration of different techniques for calculating the GCF of 14 and 28, along with insights into its broader significance and practical applications. By mastering this concept, you'll strengthen your mathematical foundation and enhance your problem-solving abilities. Remember to choose the method that best suits the numbers you're working with and the context of the problem.
Latest Posts
Latest Posts
-
What Is A Function Table
Sep 23, 2025
-
Pictures Of The Neolithic Age
Sep 23, 2025
-
Do Catabolic Reactions Release Energy
Sep 23, 2025
-
What Is A Phosphorylated Intermediate
Sep 23, 2025
-
Derivative Of 3x 2 2
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Gcf For 14 And 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.