Lcm Of 11 And 4
zacarellano
Sep 18, 2025 · 6 min read
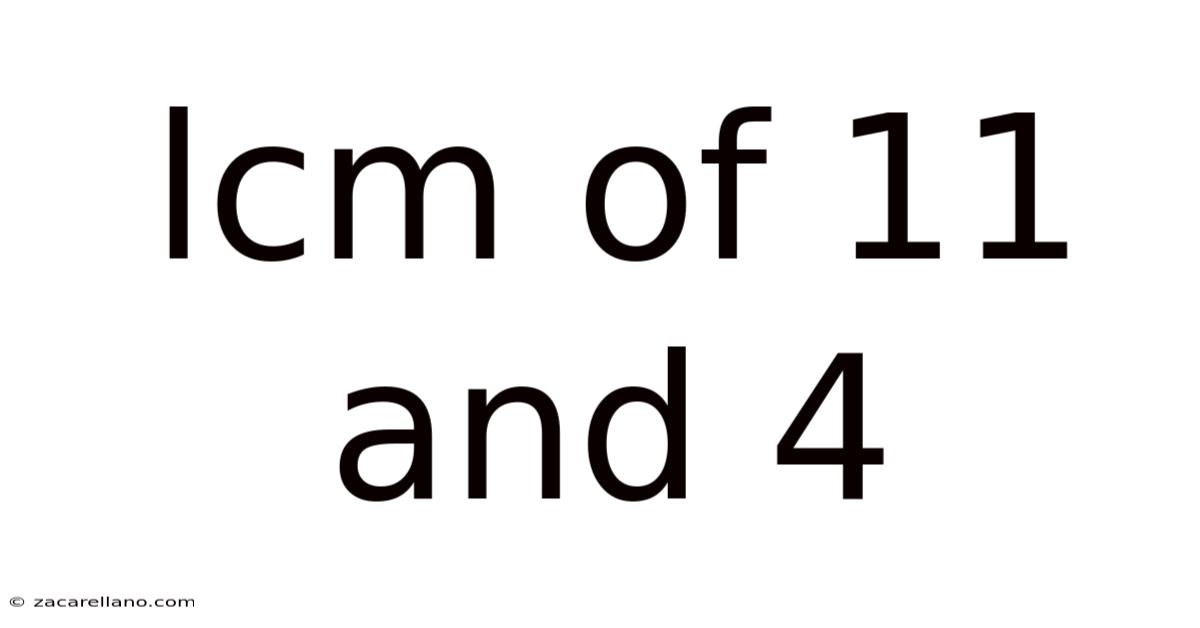
Table of Contents
Finding the Least Common Multiple (LCM) of 11 and 4: A Deep Dive
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for simplifying fractions, solving problems involving ratios and proportions, and even tackling more advanced mathematical concepts. This article will provide a comprehensive explanation of how to calculate the LCM of 11 and 4, demonstrating multiple methods and exploring the underlying mathematical principles. We'll delve into the definition of LCM, explore different calculation techniques, and address frequently asked questions. By the end, you'll not only know the LCM of 11 and 4 but also possess a solid understanding of this important mathematical concept.
Understanding Least Common Multiple (LCM)
Before we jump into calculating the LCM of 11 and 4, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Finding the LCM is particularly useful when working with fractions. When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps you find a common denominator, simplifying the process significantly. It's also essential in problems involving cycles or periodic events where you need to determine when events will occur simultaneously.
Method 1: Listing Multiples
One of the simplest methods for finding the LCM, especially for smaller numbers like 11 and 4, is by listing their multiples. Let's do this:
Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132...
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116, 120, 124, 128, 132...
Now, we look for the smallest number that appears in both lists. Notice that 44 is the smallest number common to both lists. Therefore, the LCM of 11 and 4 is 44.
This method is straightforward but can become tedious when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
A more efficient and systematic method, especially for larger numbers, is using prime factorization. This involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
-
Prime factorization of 11: 11 is a prime number itself, so its prime factorization is simply 11.
-
Prime factorization of 4: 4 = 2 x 2 = 2²
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations and multiply them together:
LCM(11, 4) = 2² x 11 = 4 x 11 = 44
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) – the largest number that divides both integers – are closely related. There's a formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
where |a x b| represents the absolute value of the product of a and b.
First, we need to find the GCD of 11 and 4. Since 11 is a prime number and 4 is not divisible by 11, the GCD of 11 and 4 is 1 (they share no common factors other than 1).
Now, we can apply the formula:
LCM(11, 4) = (|11 x 4|) / GCD(11, 4) = 44 / 1 = 44
Method 4: Using the Euclidean Algorithm (for GCD)
The Euclidean algorithm is an efficient method for finding the GCD of two numbers. While we already found the GCD of 11 and 4 to be 1, let's demonstrate the algorithm:
- Divide the larger number (11) by the smaller number (4): 11 = 2 x 4 + 3
- Replace the larger number with the smaller number (4) and the smaller number with the remainder (3): 4 = 1 x 3 + 1
- Repeat the process: 3 = 3 x 1 + 0
The last non-zero remainder is the GCD, which is 1. Then, we use the formula from Method 3 to calculate the LCM: 44/1 = 44. This method is particularly useful for finding the GCD and subsequently the LCM of larger numbers.
Why is Understanding LCM Important?
The ability to calculate the LCM extends beyond simple arithmetic problems. Here are some real-world applications:
-
Scheduling: Imagine two buses arrive at a bus stop at different intervals. Finding the LCM of their arrival intervals helps determine when they'll arrive simultaneously.
-
Fraction Operations: As mentioned earlier, the LCM is crucial for adding or subtracting fractions with unlike denominators. Without it, simplifying fractions becomes much more complex.
-
Gear Ratios: In mechanical engineering, understanding LCM is essential for calculating gear ratios and determining the optimal speed and torque combinations.
-
Music Theory: The LCM is used in music theory to determine the least common denominator for rhythmic patterns and to calculate the duration of musical phrases.
Frequently Asked Questions (FAQ)
Q: What if the numbers have common factors?
A: If the numbers share common factors, the LCM will be smaller than simply multiplying the numbers together. The methods described above, particularly prime factorization, effectively handle numbers with common factors.
Q: Can I find the LCM of more than two numbers?
A: Yes, the same principles apply. For instance, to find the LCM of 3, 4, and 6, you would first find the prime factorization of each number and then take the highest power of each prime factor present.
Q: Is there a formula to find the LCM directly without using the GCD?
A: While the GCD method is efficient, there isn't a single formula to calculate the LCM directly without considering common factors in some way, whether explicitly or implicitly. Prime factorization achieves this implicitly.
Q: Are there online calculators for LCM?
A: Yes, many online calculators can compute the LCM of numbers. However, understanding the underlying methods is crucial for deeper comprehension.
Conclusion
Calculating the LCM of 11 and 4, as demonstrated through various methods, is a foundational skill in mathematics. Understanding the different approaches—listing multiples, prime factorization, and using the GCD—provides flexibility in tackling various mathematical problems. The LCM is not merely an abstract concept; it has numerous practical applications in various fields, reinforcing the importance of mastering this fundamental mathematical idea. Remember, practice is key to improving your proficiency and understanding of this important concept. By applying these methods and understanding the principles behind them, you'll be well-equipped to tackle more complex LCM problems in the future.
Latest Posts
Latest Posts
-
Diagram Of Checks And Balances
Sep 18, 2025
-
Adam And Eve Sistine Chapel
Sep 18, 2025
-
Negative Divided By Negative Is
Sep 18, 2025
-
What Are The High Latitudes
Sep 18, 2025
-
Writing A System Of Equations
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 11 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.