Negative Divided By Negative Is
zacarellano
Sep 18, 2025 · 5 min read
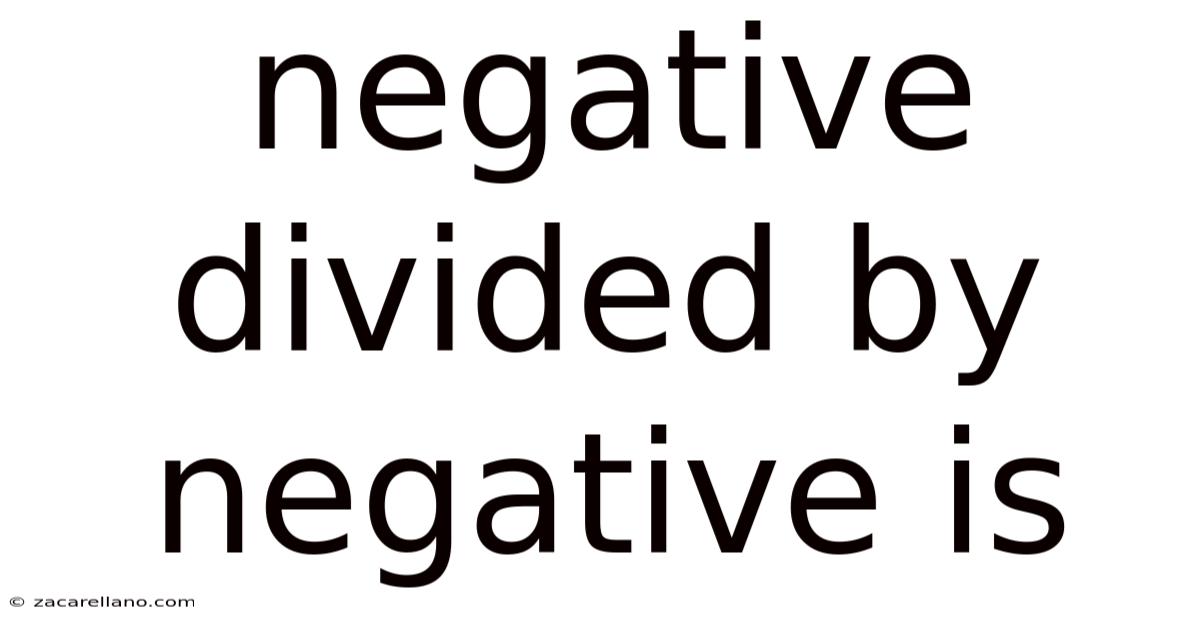
Table of Contents
Negative Divided by Negative is Positive: A Deep Dive into Integer Division
Understanding the rules of arithmetic is fundamental to mathematical literacy. While addition, subtraction, and multiplication might seem intuitive, division, especially involving negative numbers, can sometimes be confusing. This article will explore the question, "Negative divided by negative is...?" providing a comprehensive explanation, addressing common misconceptions, and demonstrating its application in various contexts. We’ll move beyond a simple answer and delve into the underlying mathematical principles that govern this seemingly simple operation.
Introduction: Why Does it Work This Way?
The core concept behind why a negative divided by a negative results in a positive number lies in the properties of multiplication and the inverse relationship between multiplication and division. Remember that division is essentially the inverse operation of multiplication. If we say 6 ÷ 2 = 3, it's the same as asking: "What number, multiplied by 2, equals 6?" The answer, of course, is 3.
This principle extends to negative numbers. Let's consider the equation -6 ÷ -2 = ?. We can rephrase this as: "What number, multiplied by -2, equals -6?" The answer is 3 because 3 x -2 = -6. This illustrates the fundamental rule: a negative number divided by a negative number always results in a positive number.
Understanding the Number Line and Opposites
Visualizing numbers on a number line can greatly aid understanding. The number line extends infinitely in both positive and negative directions. Zero sits in the middle, with positive numbers to the right and negative numbers to the left. Negative numbers represent the opposite of their positive counterparts. For instance, -3 is the opposite of 3.
This concept of opposites is crucial when considering division. When you divide by a negative number, you're essentially asking, "How many times does the negative divisor fit into the dividend?" If both numbers are negative, you're essentially "canceling out" the negativity, resulting in a positive outcome.
Stepping Through the Logic: A Step-by-Step Example
Let's solidify this concept with a real-world example. Imagine you're tracking your bank account balance. You have a debt (a negative balance) of -$60. You decide to pay off this debt in installments of -$20 each. How many installments (-$20) will it take to clear your debt (-$60)?
The calculation is: -$60 ÷ -$20 = ?
To solve this, we follow these steps:
- Ignore the signs: Consider the absolute values of the numbers: 60 ÷ 20 = 3.
- Determine the sign: Since both the dividend (-$60) and the divisor (-$20) are negative, the result will be positive.
- Combine the steps: Therefore, -$60 ÷ -$20 = +3. It will take 3 installments of -$20 to pay off your -$60 debt.
This example showcases the real-world application of this principle and how it makes intuitive sense.
Mathematical Properties and Proof
The rule for dividing negative numbers aligns with the distributive property of multiplication and division. Let's consider the expression:
(-a) / (-b) where 'a' and 'b' are positive numbers.
We can rewrite this as: (-1 * a) / (-1 * b)
Using the property of fractions, we can separate this into: (-1/-1) * (a/b)
Since (-1/-1) = 1, the expression simplifies to: 1 * (a/b) = a/b
This demonstrates that the result is positive, regardless of the initial negative signs. This mathematical proof provides a formal justification for the rule.
Beyond Integers: Extending to Rational and Real Numbers
The rule "negative divided by negative is positive" isn't limited to integers. It applies equally to rational numbers (fractions) and real numbers.
For example:
- -⅔ ÷ -⅓ = 2 (The negative signs cancel out, leaving a positive result).
- -π ÷ -2 = π/2 (Again, the negative signs cancel, and the result remains positive).
The underlying principle remains consistent: the division of two negative numbers always yields a positive result.
Common Misconceptions and How to Avoid Them
Despite the simplicity of the rule, some common misconceptions can arise:
- Confusing signs: Students often mix up the rules for addition/subtraction with those for multiplication/division. Remember that the rules are different. Adding or subtracting negative numbers follows different principles than multiplying or dividing them.
- Ignoring the signs altogether: Simply calculating the absolute values without considering the signs leads to incorrect results. Always account for the signs of the numbers involved.
- Incorrect application of the order of operations (PEMDAS/BODMAS): When dealing with complex expressions, remember to follow the order of operations correctly to prevent errors.
Frequently Asked Questions (FAQ)
Q: What happens if I divide a negative number by a positive number?
A: The result will be negative. Think of it as repeatedly subtracting the positive number from the negative number. The result will always remain negative.
Q: What happens if I divide a positive number by a negative number?
A: The result will also be negative. This is the inverse of the previous scenario.
Q: Can I use a calculator to verify the rule?
A: Yes, absolutely. Most calculators will correctly handle negative numbers in division. Use them to check your work and build confidence in your understanding.
Q: Is there a way to visualize this concept graphically?
A: While a number line helps visualize single numbers, visually representing the division of negative numbers is more complex. However, understanding the concept of opposites and the inverse relationship between multiplication and division provides a strong conceptual visualization.
Q: How does this relate to more advanced mathematical concepts?
A: This fundamental rule of arithmetic forms a basis for more advanced concepts in algebra, calculus, and linear algebra, where manipulating positive and negative numbers is crucial.
Conclusion: Mastering Negative Number Division
Mastering the rule "negative divided by negative is positive" is a crucial step in developing a solid mathematical foundation. This rule isn't just a rote memorization task; it's a logical consequence of the inverse relationship between multiplication and division and the concept of opposites. By understanding the underlying principles and practicing with various examples, you can confidently tackle problems involving negative numbers and build a strong understanding of arithmetic. This knowledge will serve as a cornerstone for more advanced mathematical studies. Remember to pay attention to the signs, follow the order of operations, and use available resources like calculators to check your work. With consistent practice and a clear grasp of the underlying concepts, you'll be well-equipped to handle any division problem, regardless of the signs involved.
Latest Posts
Latest Posts
-
Distributive Property Greatest Common Factor
Sep 18, 2025
-
Gcf Of 8 And 3
Sep 18, 2025
-
Equilibrium Potential Vs Membrane Potential
Sep 18, 2025
-
What Is Polarity Ap Bio
Sep 18, 2025
-
Dividing Fractions Worksheet And Answers
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Negative Divided By Negative Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.