Negative 7 Minus Negative 5
zacarellano
Sep 21, 2025 · 5 min read
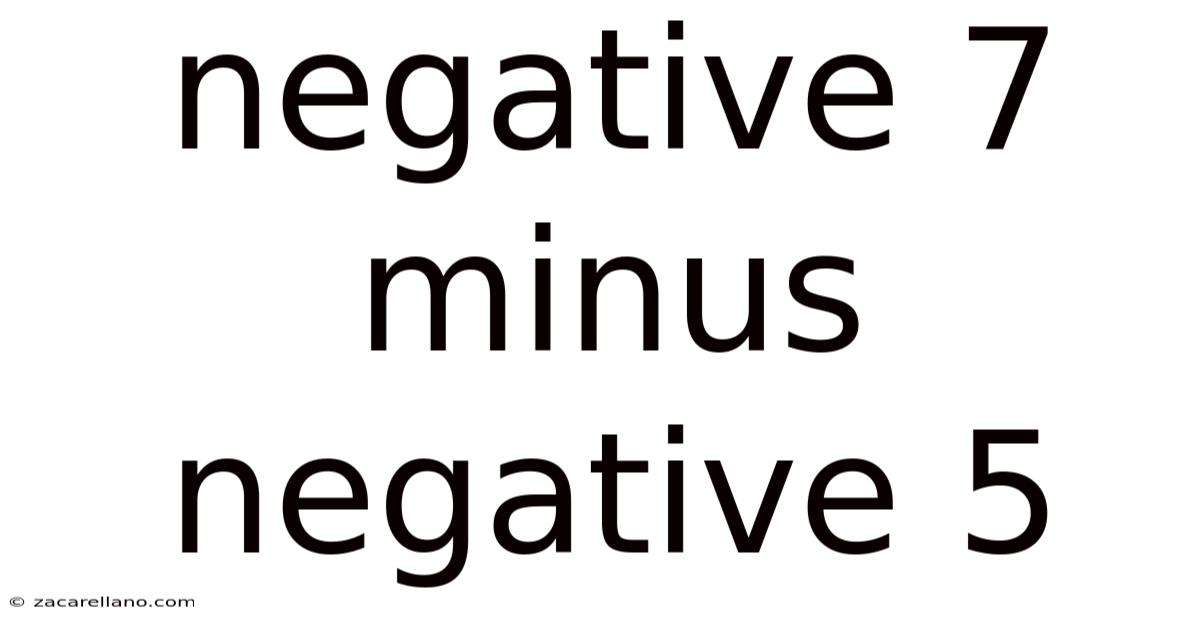
Table of Contents
Decoding the Mystery: Negative 7 Minus Negative 5
Understanding the intricacies of negative numbers can be a challenge, especially when subtraction enters the equation. This article will delve into the seemingly complex problem of negative 7 minus negative 5 (-7 - (-5)), breaking down the process step-by-step, providing visual aids, and exploring the underlying mathematical principles. By the end, you'll not only know the answer but also possess a solid understanding of subtracting negative numbers, making similar problems a breeze.
Understanding Negative Numbers
Before tackling the problem, let's refresh our understanding of negative numbers. Negative numbers represent values less than zero. They are often used to represent things like temperatures below freezing, debts, or positions below a reference point (like sea level). Think of a number line: Zero is the central point, with positive numbers extending to the right and negative numbers extending to the left.
Visualizing Subtraction
Subtraction can be visualized as taking away or removing something. If we have 5 apples and subtract 2, we're left with 3. However, subtracting negative numbers requires a slightly different perspective.
Consider the number line again. Subtraction involves moving to the left. Subtracting a positive number means moving to the left along the number line. Subtracting a negative number, surprisingly, means moving to the right. This seemingly counterintuitive concept is key to understanding the problem at hand.
The Double Negative Rule
The core of solving -7 - (-5) lies in understanding the "double negative" rule. In mathematics, two consecutive negative signs cancel each other out, transforming the expression into an addition problem.
- (-5) = +5
This rule is fundamental to working with negative numbers and is often expressed as: "A negative multiplied by a negative equals a positive."
Solving -7 - (-5) Step-by-Step
Now, let's apply this knowledge to solve our problem: -7 - (-5).
-
Identify the double negative: We see that we have "- (-5)".
-
Apply the double negative rule: This transforms "- (-5)" into "+5".
-
Rewrite the expression: Our original equation -7 - (-5) now becomes -7 + 5.
-
Perform the addition: Now we simply add -7 and 5. Imagine starting at -7 on the number line and moving 5 units to the right.
-
The Result: This leads us to -2. Therefore, -7 - (-5) = -2.
The Number Line Method
To solidify our understanding, let's visualize this on a number line:
-
Start at -7: Place your finger on -7 on the number line.
-
Subtract -5: Since we're subtracting a negative number, move your finger five units to the right.
-
End at -2: Your finger will land on -2, confirming our answer.
Different Perspectives: Adding the Opposite
Another way to approach this problem is by understanding subtraction as "adding the opposite." Instead of subtracting a number, we can add its additive inverse (its opposite). The additive inverse of a number is the number that, when added to the original number, results in zero. For example, the additive inverse of 5 is -5, and the additive inverse of -5 is 5.
Therefore, -7 - (-5) can be rewritten as -7 + (+5), which simplifies to -7 + 5, leading us to the same answer: -2.
Real-World Applications
Understanding the subtraction of negative numbers isn't just an abstract mathematical exercise; it has numerous practical applications in various fields. Here are a few examples:
-
Finance: Imagine you have a debt of $7 (-$7) and you pay off $5 (-$5). The remaining debt is calculated as -7 - (-5) = -$2.
-
Temperature: If the temperature is -7°C and it increases by 5°C, the new temperature is calculated as -7 - (-5) = -2°C.
-
Altitude: If a submarine is at -7 meters (below sea level) and ascends 5 meters, its new depth is -7 - (-5) = -2 meters.
These real-world scenarios demonstrate the importance of understanding this seemingly simple mathematical concept.
Expanding the Concept: Subtracting Larger Negative Numbers
Let's apply the same principles to a slightly more complex problem: -12 - (-8).
-
Identify the double negative: We have "- (-8)".
-
Apply the double negative rule: This becomes "+8".
-
Rewrite the expression: The equation is now -12 + 8.
-
Perform the addition: Starting at -12 and moving 8 units to the right on the number line takes us to -4.
Therefore, -12 - (-8) = -4.
Frequently Asked Questions (FAQ)
Q: Why does subtracting a negative number result in addition?
A: Subtracting a number is the same as adding its opposite. The opposite of a negative number is a positive number.
Q: Can I always rewrite subtraction as addition of the opposite?
A: Yes, this is a fundamental principle of arithmetic. It provides a consistent and efficient method for handling subtraction, especially with negative numbers.
Q: What if I'm subtracting a larger negative number from a smaller negative number?
A: The same principles apply. For instance, -5 - (-10) = -5 + 10 = 5. The result will be a positive number in this case.
Q: Are there any other ways to visualize subtracting negative numbers?
A: Yes, you can use chips or counters. Represent negative numbers with red chips and positive numbers with blue chips. Subtracting a negative chip would mean removing a red chip, effectively increasing the number of blue chips (positive value).
Q: Is there a risk of making mistakes when applying the double negative rule?
A: While the double negative rule is straightforward, paying attention to signs is crucial. Double-check your work to avoid errors.
Conclusion: Mastering Negative Number Subtraction
Mastering the subtraction of negative numbers is a crucial step in developing a strong foundation in mathematics. By understanding the double negative rule and visualizing the process using a number line or other methods, you can confidently tackle any problem involving the subtraction of negative numbers. Remember, practice is key. Try solving various problems to reinforce your understanding and build your problem-solving skills. This article aimed to provide a comprehensive understanding, moving beyond simply stating the answer to fostering a deeper appreciation for the underlying mathematical principles. Remember, the journey of learning is continuous, and every step forward, no matter how small, contributes to a greater understanding of the mathematical world.
Latest Posts
Latest Posts
-
Standing Wave In A Pipe
Sep 21, 2025
-
V Pi R 2 H
Sep 21, 2025
-
Gcf Of 56 And 16
Sep 21, 2025
-
Ap World Unit 5 Review
Sep 21, 2025
-
Bonds Broken Minus Bonds Formed
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Negative 7 Minus Negative 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.