V 2 Vo 2 2ax
zacarellano
Sep 15, 2025 · 7 min read
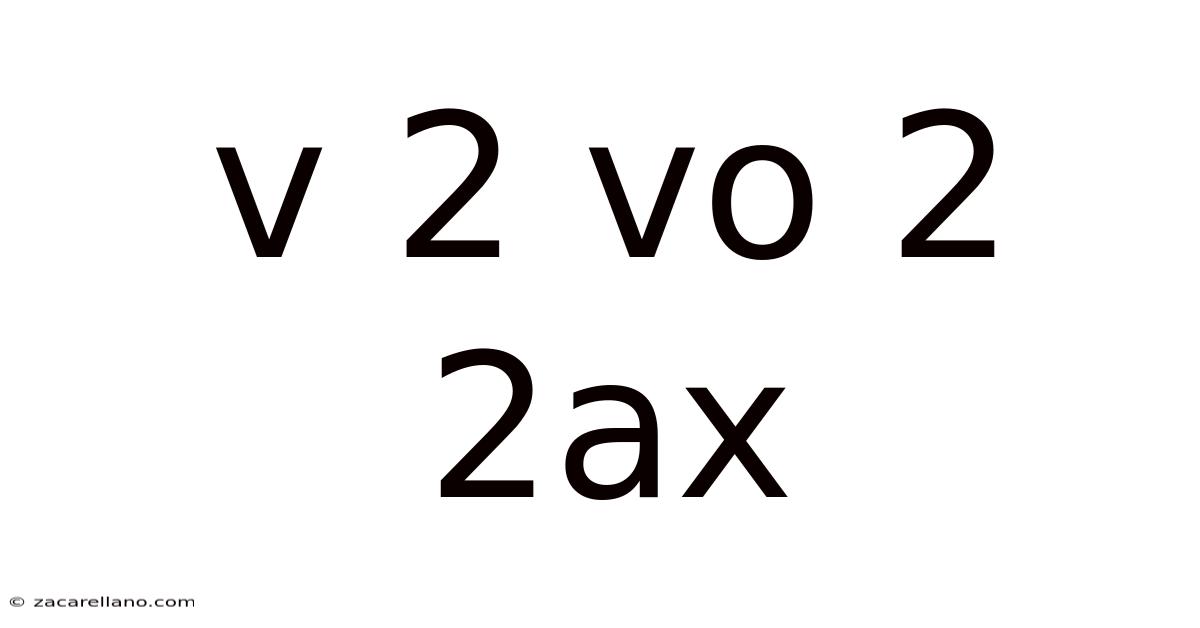
Table of Contents
Understanding V² = U² + 2aS: A Deep Dive into Constant Acceleration
This article provides a comprehensive explanation of the equation V² = U² + 2aS, a cornerstone of classical mechanics used to describe motion under constant acceleration. We'll explore its derivation, application, and practical implications, ensuring a thorough understanding for students and enthusiasts alike. This equation is crucial for solving problems involving constant acceleration in one dimension. We will cover various scenarios and address frequently asked questions.
Introduction: Unveiling the Equation
The equation V² = U² + 2aS is a kinematic equation that relates the final velocity (V) of an object to its initial velocity (U), acceleration (a), and displacement (s). This equation is particularly useful when you know the initial and final velocities, along with the acceleration, and you need to find the displacement or vice-versa. It's vital to remember that this equation only applies to situations with constant acceleration. If the acceleration changes, you'll need to use calculus-based methods.
The variables in the equation represent:
- V: Final velocity (m/s) – the velocity the object reaches at the end of the considered time interval.
- U: Initial velocity (m/s) – the velocity the object starts with at the beginning of the considered time interval.
- a: Acceleration (m/s²) – the rate at which the object's velocity changes. Remember that acceleration can be positive (speeding up) or negative (slowing down).
- s: Displacement (m) – the change in position of the object during the time interval. This is the distance traveled along the line of motion, and it’s a vector quantity (meaning it has both magnitude and direction).
Derivation of V² = U² + 2aS
The derivation of this equation relies on two other fundamental kinematic equations:
-
V = U + at: This equation gives the final velocity (V) of an object after a time (t) under constant acceleration (a).
-
s = Ut + ½at²: This equation gives the displacement (s) of an object after a time (t) under constant acceleration (a).
Let's derive V² = U² + 2aS:
-
Solve for t in equation 1: We can rearrange V = U + at to solve for time (t): t = (V - U) / a.
-
Substitute into equation 2: Substitute the expression for t from step 1 into the second equation (s = Ut + ½at²):
s = U[(V - U) / a] + ½a[(V - U) / a]²
-
Simplify the equation: Now, we simplify this expression through algebraic manipulation:
s = (UV - U²) / a + ½a(V² - 2UV + U²) / a²
s = (UV - U²) / a + (V² - 2UV + U²) / (2a)
Multiplying both sides by 2a to eliminate the fractions:
2as = 2UV - 2U² + V² - 2UV + U²
-
Final Result: After simplification, we arrive at our desired equation:
V² = U² + 2as
Applications of V² = U² + 2aS
The equation V² = U² + 2aS finds widespread applications in various scenarios involving constant acceleration. Here are some examples:
-
Calculating stopping distances: This is crucial in traffic safety studies and driver education. Knowing the initial velocity of a vehicle and its deceleration rate (negative acceleration), we can calculate the minimum stopping distance.
-
Projectile motion (vertical component): While projectile motion involves two-dimensional movement, the vertical component of motion is often analyzed using this equation, assuming constant gravitational acceleration. We can calculate the maximum height reached by a projectile or its final velocity just before hitting the ground.
-
Analyzing the motion of falling objects: For objects falling freely under gravity (ignoring air resistance), we can use this equation to determine their final velocity after falling a certain distance. Remember to use the appropriate sign for acceleration (usually -9.8 m/s² near the Earth's surface).
-
Analyzing collisions: In certain types of collisions (especially those involving inelastic collisions), we can use this equation to estimate changes in velocity after the impact, considering the impulse imparted and the distance involved.
-
Engineering applications: This equation is fundamental in various engineering disciplines, including mechanical, civil, and aerospace engineering, to analyze and design systems involving movement under constant acceleration. Examples include designing ramps, calculating braking systems for vehicles, and analyzing the motion of rockets.
Solving Problems using V² = U² + 2aS
Let's consider a few examples to demonstrate the practical application of the equation:
Example 1: A car accelerates uniformly from rest (U = 0 m/s) to a final velocity of 20 m/s over a distance of 100 meters. Calculate the acceleration of the car.
- Known: U = 0 m/s, V = 20 m/s, s = 100 m
- Unknown: a
- Solution: Using V² = U² + 2as, we have: (20)² = (0)² + 2a(100). Solving for 'a', we get a = 2 m/s².
Example 2: A ball is thrown vertically upward with an initial velocity of 15 m/s. Ignoring air resistance, what is the maximum height the ball reaches before momentarily coming to a stop? (Use g = 9.8 m/s² as the acceleration due to gravity).
- Known: U = 15 m/s, V = 0 m/s (at the maximum height), a = -9.8 m/s²
- Unknown: s (maximum height)
- Solution: Using V² = U² + 2as, we have: (0)² = (15)² + 2(-9.8)s. Solving for 's', we get s ≈ 11.5 m.
Example 3: A train traveling at 30 m/s begins to decelerate uniformly at a rate of -2 m/s². How far will it travel before coming to a complete stop?
- Known: U = 30 m/s, V = 0 m/s, a = -2 m/s²
- Unknown: s
- Solution: Using V² = U² + 2as, we have: (0)² = (30)² + 2(-2)s. Solving for 's', we get s = 225 m.
Limitations and Considerations
While V² = U² + 2aS is a powerful tool, it's crucial to remember its limitations:
-
Constant Acceleration: The equation only applies to situations with constant acceleration. If acceleration changes over time, more advanced methods (e.g., calculus) are needed.
-
One Dimension: The equation is applicable to motion in one dimension only. For two-dimensional or three-dimensional motion, vector analysis is required.
-
Neglect of External Forces: In many applications (like the projectile motion example), external forces like air resistance are ignored for simplification. In real-world situations, these forces can significantly affect the motion.
Frequently Asked Questions (FAQ)
Q1: What happens if the acceleration is zero?
A1: If the acceleration (a) is zero, the equation simplifies to V² = U², implying that the final velocity equals the initial velocity. This means there is no change in velocity, and the object is moving at a constant speed.
Q2: Can this equation be used for motion in two dimensions?
A2: No, this equation is only applicable for motion in one dimension. For two-dimensional motion (like projectile motion), you need to analyze the x and y components separately, applying this equation to each component with its respective acceleration.
Q3: How do I handle situations with negative acceleration (deceleration)?
A3: Simply use a negative value for 'a' in the equation. The negative sign indicates that the object is slowing down.
Q4: What if I don't know the time?
A4: This equation is specifically designed for situations where you don't know the time but have information about the initial and final velocities, acceleration, and displacement. If you knew the time, you would likely use the other kinematic equations.
Q5: What are the units for each variable?
A5: The units must be consistent throughout. Typically, the units are: V and U (m/s), a (m/s²), and s (m).
Conclusion: Mastering Constant Acceleration Motion
The equation V² = U² + 2aS is a fundamental tool in understanding and analyzing motion under constant acceleration. By understanding its derivation, applications, and limitations, you can confidently solve a wide range of problems in physics and engineering. Remember to always consider the context of the problem, ensure consistent units, and be aware of the assumptions made (primarily the assumption of constant acceleration). Mastering this equation will solidify your understanding of classical mechanics and prepare you for more complex problems in the future. Through careful application and understanding of its limitations, this equation proves invaluable in various fields.
Latest Posts
Latest Posts
-
How To Divide Complex Fractions
Sep 15, 2025
-
Objectives For Verbs Lesson Plans
Sep 15, 2025
-
Positive Feedback Loop Endocrine System
Sep 15, 2025
-
Gcf Of 35 And 15
Sep 15, 2025
-
Woman Holding A Balance Painting
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about V 2 Vo 2 2ax . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.