X 2 6x 10 0
zacarellano
Sep 19, 2025 · 6 min read
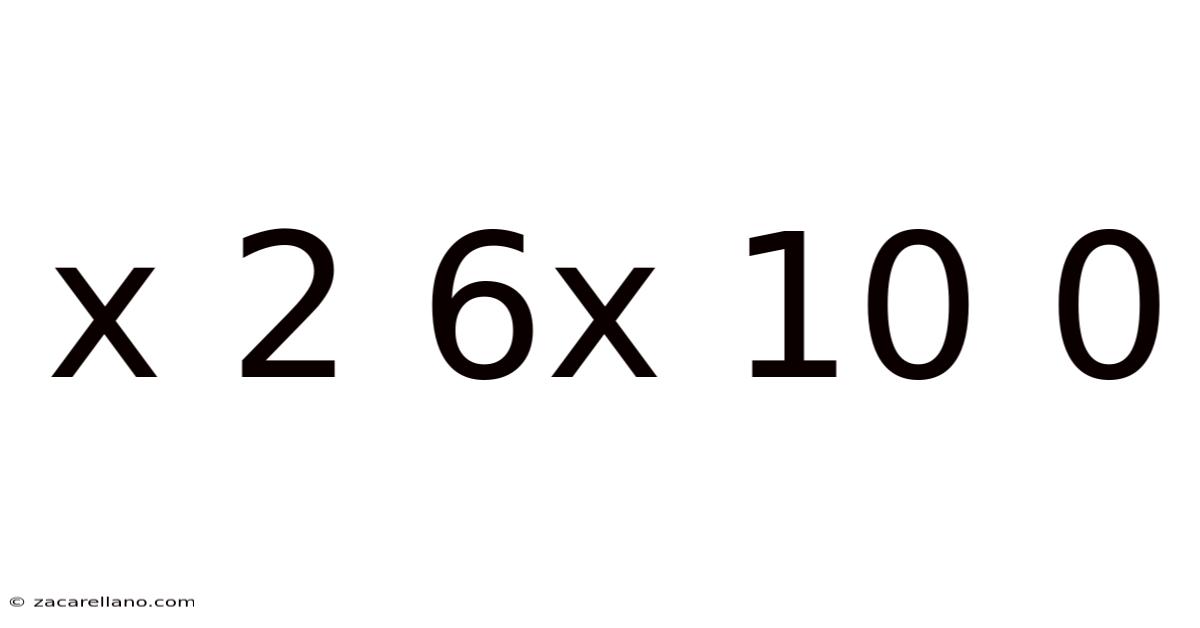
Table of Contents
Deconstructing the Expression: x² + 6x + 10 = 0
This article delves into the quadratic expression x² + 6x + 10 = 0, exploring its various aspects, from basic understanding to advanced techniques for solving and interpreting its solutions. We will cover methods like factoring, completing the square, and the quadratic formula, ultimately revealing the nature of its roots and their significance in mathematics and related fields. Understanding this seemingly simple equation provides a strong foundation for tackling more complex mathematical problems.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our specific equation, x² + 6x + 10 = 0, fits this mold with a = 1, b = 6, and c = 10. Solving quadratic equations means finding the values of x that satisfy the equation—in other words, the values of x that make the equation true. These values are called the roots or solutions of the equation.
Method 1: Attempting to Factor the Quadratic
Factoring is a straightforward method for solving quadratic equations, but it's only applicable when the equation can be easily factored into two linear expressions. We look for two numbers that add up to 'b' (6 in our case) and multiply to 'c' (10). Let's try to find such numbers.
We need two numbers that add to 6 and multiply to 10. The pairs of factors of 10 are (1, 10), (2, 5), (-1, -10), and (-2, -5). None of these pairs add up to 6. Therefore, this quadratic equation cannot be factored using integer coefficients. This means we need to explore alternative methods.
Method 2: Completing the Square
Completing the square is a powerful technique that works for all quadratic equations. The goal is to manipulate the equation into a perfect square trinomial, which can then be easily solved. Here's how it works for x² + 6x + 10 = 0:
-
Move the constant term to the right side: Subtract 10 from both sides: x² + 6x = -10
-
Find the value to complete the square: Take half of the coefficient of x (which is 6), square it (3² = 9), and add it to both sides: x² + 6x + 9 = -10 + 9
-
Rewrite the left side as a perfect square: (x + 3)² = -1
-
Solve for x: Take the square root of both sides: x + 3 = ±√(-1)
This introduces the imaginary unit, denoted as 'i', where i² = -1. Therefore, x + 3 = ±i, and solving for x gives us:
x = -3 + i and x = -3 - i
These are the two complex conjugate roots of the quadratic equation. Complex numbers have a real part and an imaginary part. In this case, the real part is -3, and the imaginary parts are +i and -i.
Method 3: Using the Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 6, c = 10), we get:
x = [-6 ± √(6² - 4 * 1 * 10)] / (2 * 1)
x = [-6 ± √(36 - 40)] / 2
x = [-6 ± √(-4)] / 2
x = [-6 ± 2i] / 2
x = -3 ± i
This confirms the results we obtained using the completing the square method. The roots are again -3 + i and -3 - i.
The Discriminant and the Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. It determines the nature of the roots:
- If b² - 4ac > 0: The equation has two distinct real roots.
- If b² - 4ac = 0: The equation has one real root (a repeated root).
- If b² - 4ac < 0: The equation has two complex conjugate roots.
In our case, b² - 4ac = 36 - 40 = -4, which is less than 0. This confirms that the equation has two complex conjugate roots, as we've already found.
Graphical Representation and Interpretation
The graph of a quadratic equation is a parabola. The x-intercepts of the parabola represent the real roots of the equation. Since our equation has complex roots, its parabola does not intersect the x-axis. The parabola opens upwards (because a = 1 > 0) and its vertex lies above the x-axis. The vertex represents the minimum value of the quadratic function. The x-coordinate of the vertex can be found using the formula -b/2a = -6/(2*1) = -3. The y-coordinate is obtained by substituting x = -3 into the equation: (-3)² + 6(-3) + 10 = 1. Therefore, the vertex is at (-3, 1).
Applications of Quadratic Equations
Quadratic equations have widespread applications in various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stresses and strains in materials.
- Economics: Modeling cost functions, optimizing production levels.
- Computer Graphics: Creating curves and shapes.
Frequently Asked Questions (FAQ)
Q: What are complex numbers?
A: Complex numbers are numbers that can be expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). 'a' is called the real part, and 'b' is called the imaginary part.
Q: Why are complex conjugate roots always found in pairs?
A: The fundamental theorem of algebra states that a polynomial of degree n has exactly n roots (counting multiplicity). Complex roots of polynomials with real coefficients always come in conjugate pairs. This means if a + bi is a root, then a - bi is also a root.
Q: Can I solve this equation using a graphing calculator?
A: Yes, a graphing calculator can be used to find the approximate solutions graphically by plotting the function y = x² + 6x + 10 and observing where it intersects the x-axis (which it won't in this case, as we've seen). However, it may not directly give you the complex roots.
Q: What is the significance of the vertex of the parabola?
A: The vertex represents the minimum (or maximum, if the parabola opens downwards) value of the quadratic function. This is crucial in optimization problems where we need to find the minimum or maximum value of a quantity.
Conclusion: Beyond the Equation
While seemingly a simple mathematical expression, x² + 6x + 10 = 0 offers a rich learning experience. It showcases the various methods for solving quadratic equations, highlights the importance of the discriminant in determining the nature of the roots, and introduces the concept of complex numbers. Furthermore, it underscores the broader applications of quadratic equations in diverse fields. Understanding this equation serves as a strong foundation for tackling more intricate mathematical concepts and problem-solving scenarios. The journey from attempting to factor to employing the quadratic formula and interpreting the complex roots demonstrates the multifaceted nature of even seemingly basic mathematical problems. The exploration of the graphical representation further enriches the understanding of the equation's behavior and its real-world applications.
Latest Posts
Latest Posts
-
Noble Gas Configuration For Bismuth
Sep 19, 2025
-
Negative 1 Minus Negative 4
Sep 19, 2025
-
What Weighs About 1 Pound
Sep 19, 2025
-
What Is The Strongest Imf
Sep 19, 2025
-
Difference Between Substitutes And Complements
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 6x 10 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.