Factor X 2 8x 7
zacarellano
Sep 13, 2025 · 7 min read
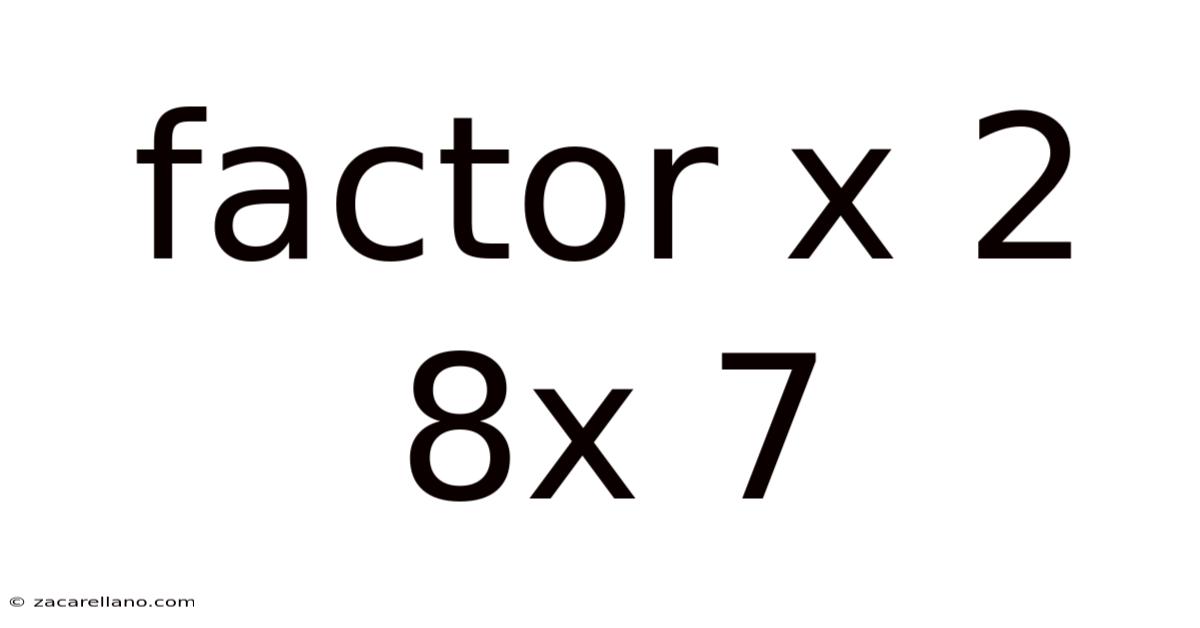
Table of Contents
Unraveling the Mystery: A Deep Dive into the Quadratic Expression x² + 8x + 7
The seemingly simple quadratic expression, x² + 8x + 7, offers a gateway to understanding fundamental concepts in algebra. This article will delve into its various aspects, from basic factorization and solving for x to exploring its graphical representation and real-world applications. We'll cover everything from the step-by-step process of factoring to deeper mathematical explanations, ensuring a comprehensive understanding for students of all levels. Whether you're struggling with quadratics or looking to solidify your understanding, this guide will equip you with the knowledge and tools to master this important algebraic concept.
Understanding Quadratic Expressions
Before we jump into factoring x² + 8x + 7, let's establish a foundational understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our example, x² + 8x + 7, a = 1, b = 8, and c = 7.
Key Terminology:
- Coefficient: The numerical factor of a term (e.g., 1 in x², 8 in 8x, and 7 in 7).
- Variable: The symbol representing an unknown value (in this case, x).
- Constant: A term without a variable (in this case, 7).
- Roots/Zeros: The values of x that make the expression equal to zero. These are also the x-intercepts of the parabola representing the quadratic equation.
Factoring x² + 8x + 7: A Step-by-Step Approach
Factoring a quadratic expression involves rewriting it as a product of two simpler expressions. This process is crucial for solving quadratic equations and simplifying more complex algebraic manipulations. There are several methods for factoring quadratics, but for x² + 8x + 7, the easiest approach is using the following steps:
-
Identify the factors of 'c' that add up to 'b': In our expression, c = 7 and b = 8. We need to find two numbers that multiply to 7 and add up to 8. The only pair of integers that satisfies this condition is 1 and 7 (1 x 7 = 7 and 1 + 7 = 8).
-
Rewrite the expression using the identified factors: Now, we rewrite the middle term (8x) using the factors we found:
x² + 1x + 7x + 7
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(x + 1) + 7(x + 1)
-
Factor out the common binomial: Notice that both terms now share the binomial (x + 1). Factor this out:
(x + 1)(x + 7)
Therefore, the factored form of x² + 8x + 7 is (x + 1)(x + 7). This means the expression can be represented as the product of two binomials: (x + 1) and (x + 7).
Solving the Quadratic Equation x² + 8x + 7 = 0
Once we have factored the quadratic expression, we can easily solve the corresponding quadratic equation, x² + 8x + 7 = 0. To find the roots (or zeros) of the equation, we set each factor equal to zero and solve for x:
- x + 1 = 0 => x = -1
- x + 7 = 0 => x = -7
Therefore, the solutions to the quadratic equation x² + 8x + 7 = 0 are x = -1 and x = -7. These values represent the points where the parabola intersects the x-axis.
Graphical Representation: The Parabola
Quadratic expressions are graphically represented by parabolas. A parabola is a U-shaped curve that opens upwards if 'a' (the coefficient of x²) is positive and downwards if 'a' is negative. In our case, a = 1 (positive), so the parabola opens upwards.
The vertex of the parabola is the lowest point (or highest point if the parabola opens downwards). The x-coordinate of the vertex can be found using the formula: x = -b / 2a. In our case, this is x = -8 / (2 * 1) = -4. The y-coordinate can be found by substituting this x-value back into the original equation: y = (-4)² + 8(-4) + 7 = -9. Therefore, the vertex of the parabola is (-4, -9).
The x-intercepts of the parabola are the points where the parabola crosses the x-axis. These are the roots of the quadratic equation, which we already found to be -1 and -7. The y-intercept is the point where the parabola crosses the y-axis, which occurs when x = 0. Substituting x = 0 into the equation gives y = 7. Therefore, the y-intercept is (0, 7). By plotting these points and the vertex, we can accurately sketch the parabola.
The Mathematical Significance of Factoring
Factoring quadratic expressions isn't just about finding the solutions to equations; it reveals crucial information about the expression's behavior and properties. The factored form (x + 1)(x + 7) shows us the roots directly. It also helps in:
- Simplifying expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and solve.
- Finding the roots (zeros): As demonstrated, factoring directly provides the roots of the quadratic equation.
- Determining the x-intercepts: The roots correspond to the x-intercepts of the parabola, providing key graphical information.
- Solving real-world problems: Quadratic equations model numerous real-world scenarios, from projectile motion to area calculations, and factoring is crucial for solving these problems.
Real-World Applications
Quadratic expressions and equations appear frequently in various real-world scenarios. Here are a few examples:
- Projectile Motion: The trajectory of a projectile (like a ball thrown in the air) can be modeled using a quadratic equation. Factoring helps determine the time it takes for the projectile to reach the ground (when the height is zero).
- Area Calculations: If you have a rectangular area with a given perimeter and want to find the dimensions that maximize the area, you'll likely encounter a quadratic equation.
- Physics and Engineering: Quadratic equations are essential in many physics and engineering applications, such as modeling the motion of objects under the influence of gravity, calculating the strength of structures, and analyzing electrical circuits.
- Economics and Finance: Quadratic functions can model cost, revenue, and profit functions, helping businesses optimize their operations and make informed decisions.
Frequently Asked Questions (FAQ)
Q: What if the quadratic expression cannot be factored easily?
A: If a quadratic expression cannot be easily factored using the methods described above, you can use the quadratic formula: x = [-b ± √(b² - 4ac)] / 2a. This formula will always provide the solutions, even if the expression is not easily factorable.
Q: What is the significance of the discriminant (b² - 4ac)?
A: The discriminant determines the nature of the roots. If b² - 4ac > 0, there are two distinct real roots. If b² - 4ac = 0, there is one real root (a repeated root). If b² - 4ac < 0, there are no real roots (the roots are complex numbers). In our example, b² - 4ac = 64 - 28 = 36 > 0, indicating two distinct real roots.
Q: Can I use other methods to factor quadratic expressions?
A: Yes, other methods exist, such as completing the square and using the AC method. However, for simpler expressions like x² + 8x + 7, the method explained above is often the most straightforward.
Q: What happens if 'a' is not equal to 1?
A: If 'a' is not equal to 1, the factoring process becomes slightly more complex but follows similar principles. You might need to use techniques like the AC method or factoring by grouping to find the appropriate factors.
Conclusion
The seemingly simple quadratic expression x² + 8x + 7 opens up a rich understanding of fundamental algebraic concepts. Through factoring, we can readily solve the corresponding quadratic equation, determine the characteristics of its graphical representation (the parabola), and appreciate its significant applications in various fields. By mastering the techniques outlined in this article, you'll gain a robust foundation in algebra, empowering you to tackle more complex mathematical problems and real-world challenges. Remember to practice regularly, explore different approaches, and don't hesitate to ask for help when needed. The journey to mastering algebra is a rewarding one, filled with fascinating discoveries and practical applications.
Latest Posts
Latest Posts
-
Whats Bigger 3 8 Or 1 2
Sep 13, 2025
-
Orden De Las Operaciones Matematicas
Sep 13, 2025
-
Gcf Of 15 And 35
Sep 13, 2025
-
4 Places Us Used Imperialism
Sep 13, 2025
-
Covalent Bond Metal To Nonmetal
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.